In this post, we'll take a look at what it is quadratic equation, what conditions must be met to solve them, and how to calculate the discriminant (delta), which determines the number of solutions. We will also discuss examples of step-by-step calculations that can be easily done with a quadratic equation calculator. You'll learn about equations with one, two or no solutions, and how to effectively use tools that make solving them easier.

In this entry:

1. What is a quadratic equation
2. Solvability condition
3. The discriminant (delta) of a quadratic equation
4. Example solutions from the calculator

Quadratic equation

A quadratic equation (with one unknown x) is called an equation that can be brought to the form :

with a,b,c being fixed real numbers and a≠0.

Solvability condition

The number of solutions in a quadratic equation depends on the value of the discriminant (delta) as follows:

• ∆<0 - no solutions
• ∆=0 - one solution
• ∆>0 - two solutions

The discriminant (delta) of a quadratic equation

The discriminant of a quadratic equation is also called the delta (Δ). The two names can be used interchangeably.

If a quadratic equation has two solutions, we calculate them as follows. In the first step, let's calculate the delta for the equation using the formula:

We then calculate the solutions to the equation from the formulas below:

Examples of solutions from a quadratic equation calculator

Below I have included an example of solving a quadratic equation.

The results of the example solutions were obtained using free calculator Quadratic Equations

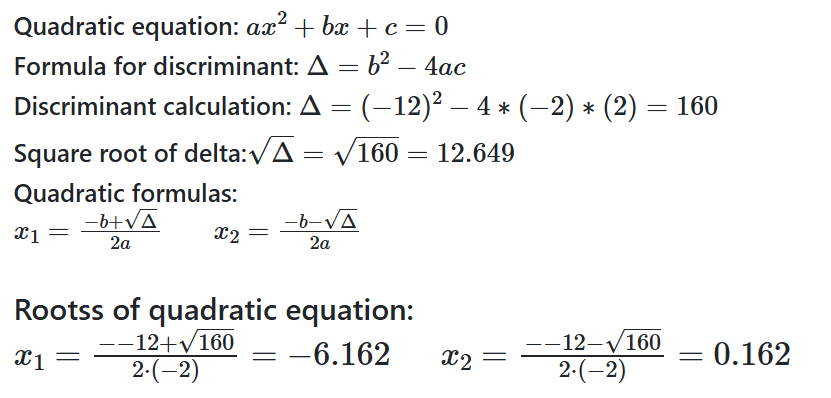
The solutions of a quadratic equation are also called roots of the quadratic equation.

If this quadratic equation has single solution (double)

Below is an example of solving a quadratic equation with one double solution.

You are invited to use free quadratic equation calculator. Thank you